jomo.org

Grenzkosten

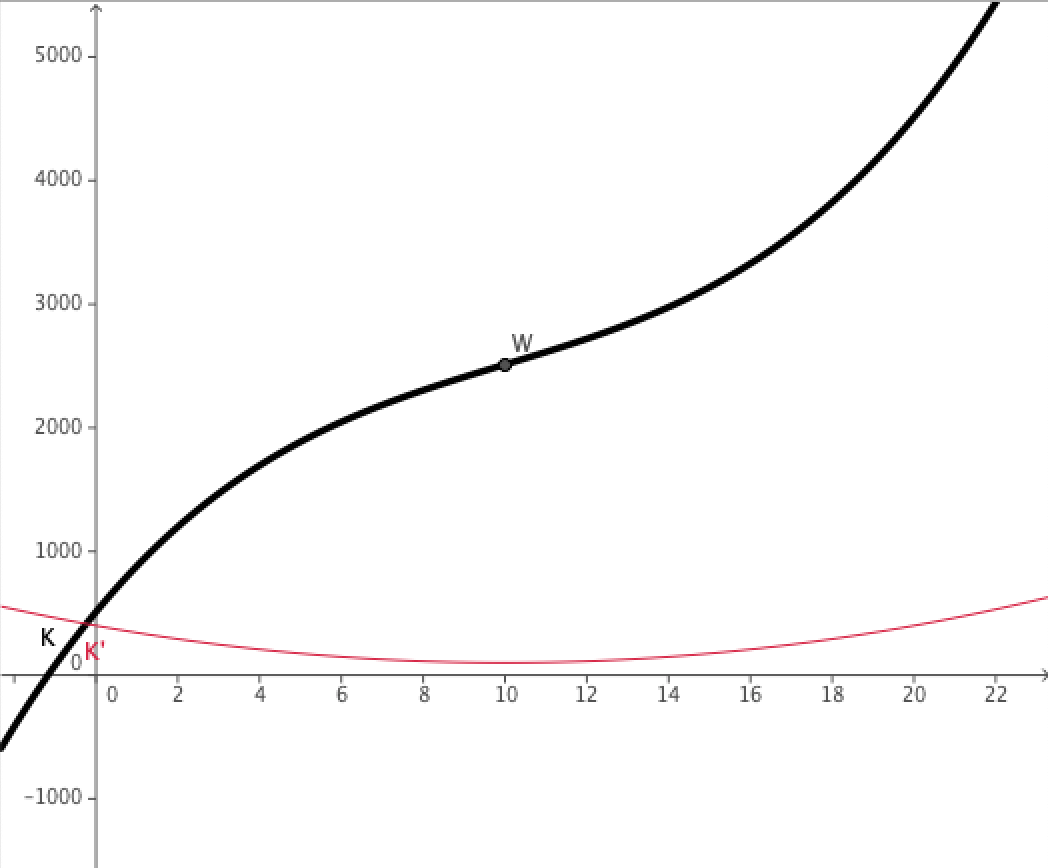
Die erste Ableitung der Kostenfunktion zeigt die Kostenzuwächse. Man nennt die Kostenzuwächse Grenzkosten, die erste Ableitung heißt Grenzkostenfunktion.

Der Wendepunkt der Kostenfunktion gibt Produktionsmenge an, für die die Grenzkosten (Kostenzuwachs bei Produktionsausweitung) am Geringsten sind. Diese Produktionsmenge heißt Kostenkehre.

Stückkosten

Die Stückkostenfunktion zeigt, dass und wie die Höhe der Stückkosten von der Produktionsmenge abhängt. Die Stückkosten nehmen (in diesem Beispiel) mit zunehmender Produktionsmenge ab, ab einer bestimmten Produktionsmenge allerdings nehmen sie wieder zu.

Die Stückkosten sind wichtig, weil sie den minimalen Verkaufspreis pro Stück an geben. Bei unterschiedlichen Produktionsmengen gibt es also unterschiedliche minimale Verkaufspreise! Wenn ein Betrieb den geringstmöglichen Verkaufspreis (ohne Verlust) sucht, berechnet er das Minimum der Stückkostenfunktion. Achtung: Dieser minimale Verkaufspreis ist nur bei einer bestimmten Produktionsmenge gültig. Diese Produktionsmenge heißt Betriebsoptimum, der Verkaufspreis heißt langfristige Preisuntergrenze.

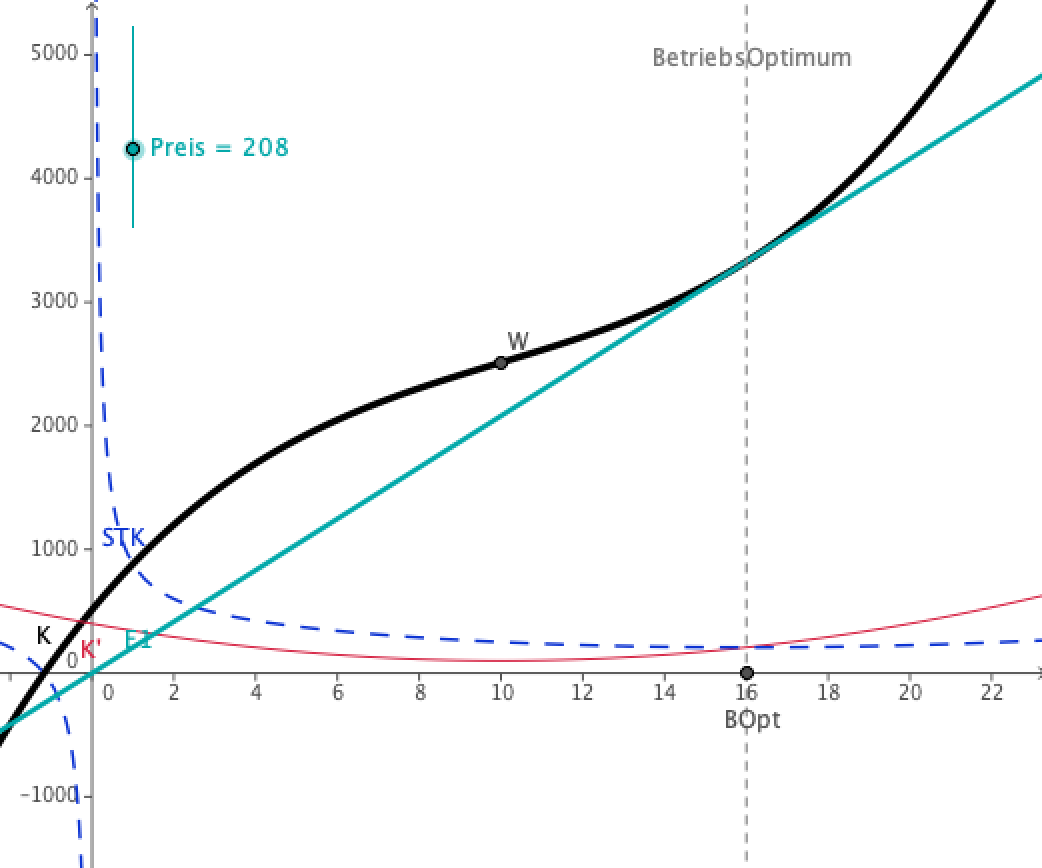
Setzt man als Preis die langfristige Preisuntergrenze in die Erlösfunktion E(x)= px ein, so erhält man eine Erlösfunktion, die die Kostenfunktion im Betriebsoptimum berührt. Das entspricht der Definition der langfristigen Preisuntergrenze als minimalem Verkaufspreis, bei dem weder Gewinn noch Verlust erzielt wird.

Variable (Stück-)Kosten

Die variablen Kosten sind jene Kosten, die von der Produktionsmenge abhängig sind. Mathematisch sind das jene Teile des Funktionsterms mit einem x. Dividiert man die variablen Kosten durch x, erhält man die variable Stückkostenfunktion VSTK(x). Die Produktionsmenge beim Minimum von VSTK(x) heißt Betriebsminimum, der y-Wert heißt kurzfristige Preisuntergrenze. Unter der Voraussetzung, dass andere Produkte die Fixkosten tragen, ist der Verkauf zu diesem eigentlich defizitären Preis (kurzfristig) wirtschaftlich sinnvoll.

Die Gerade durch den Fixkostenpunkt berührt die Kostenfunktion im Betriebsminimum. Das entspricht der gleiche Stelle, an der die um die Fixkosten nach unten verschobene variable Kostenfunktion von der Erlösfunktion mit der kurzfrisitgen Preisuntergrenze als Verkaufspreis berührt wird.

In der obigen Abbildung stellt man sich die x-Achse um die Fixkosten hinaufverschoben vor. Man bildet eine neue Erlösfunktion, die die Kostenfunktion als Tangente berührt und erhält so das Betriebsminimum. Die variable Stückkosten verläuft etwas unterhalb der Stückkostenfunktion.

Grenzkosten, Stückkosten und variable Stückkosten

Interessanterweise schneidet die Grenzkostenfunktion die Stückkosten- und die variable Stückkostenfunktion in deren Minimum, also im Betriebsoptimum und im Betriebsminimum. Das kann über das Verhältnis von (variablen) Stückkosten und Grenzkosten bei Produktionsausweitung erklärt werden.

Kosten, Preis und Gewinn

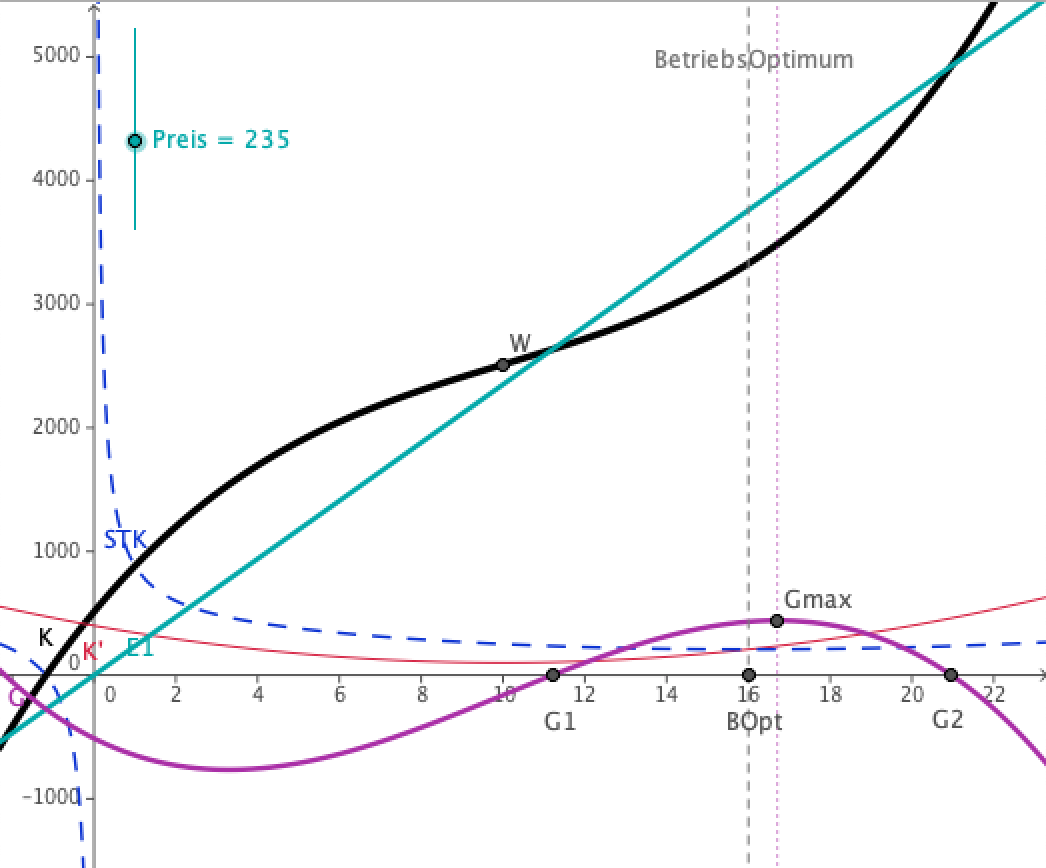
Für einen Betrieb wichtig ist noch die Produktionsmenge für den maximalen Gewinn. Setzt man in die Erlösfunktion einen höheren Preis als die langfristige Preisuntergrenze ein, so erhält man eine Erlösfunktion, die die Kostenfunktion echt schneidet und daher einen Gewinnbereich ermöglicht. Das Maximum der Gewinnfunktion liegt mengenmäßig etwas oberhalb des Betriebsoptimums. Setzt man als Preis die langfristige Preisuntergrenze ein, so fallen Menge für den maximalen Gewinn und Betriebsoptimum zusammen, der maximale Gewinn beträgt Null. Die Gewinnfunktin berührt die x-Achse an dieser Stelle von unten.

Aufgabenstellungen zur Kostentheorie bei gegebenem Funktionsterm

Kubische Kostenfunktion

• Berechne die Kostenkehre und die Grenzkosten bei der Kostenkehre
• Berechne die Grenzkosten bei anderen Produktionsmengen (etwa 10, 20 30 ME)
• Berechne die Stückkostenfunktion, das Betriebsoptimum und die langfristige Preisuntergrenze.
• Berechne die Stückkosten bei anderen Produktionsmengen.
• Wie groß muss der Verkaufspreis bei einer Produktion von … ME mindestens sein?
• Berechne das Betriebsminimum und die kurzfrisitge Preisuntergrenze.
• Berechne die variablen Stückkosten bei verschiedenen Produktionsmengen.
• Wähle einen sinnvollen Verkaufspreis, bilde die Erlösfunktion und berechne die Gewinnfunktion, die Gewinnschwellen, die Produktionsmenge für den maximalen Gewinn und den maximalen Gewinn!

Quadratische bzw. lineare Kostenfunktion

• Untersuche, wie sich bei einer quadratischen (progressiven) Kostenfunktion bzw. bei linearen Kostenfunktion Grenzkosten, Stückkosten und variable Stückkosten verhalten. Was läßt sich über Kostenkehre, Betriebsoptimum und Betriebsminmum sagen?
• Was läßt sich bei quadratischen bzw. linearen Kostenfunktionen über minimalen Verkaufspreis, Erlös- und Gewinnfunktion bzw. maximalen Gewinn sagen?

Beispiele für kubische Kostenverläufe
K(x) = 0,05x³ – 3x² + 80x + 100
K(x) = 1,00x³ – 10x² + 50x + 150
K(x) = 1,00x³ – 12x² + 60x + 200

Beispiele für quadratische Kostenverläufe
K(x) = x² + 50x + 500
K(x) = x² + 40x + 400
K(x) = x² + 30x + 300

Beispiele für lineare Kostenverläufe
K(x) = 0,5x + 10
K(x) = 2,5x + 20
K(x) = 5,0x + 30