Einführung: Seitenverhältnisse und Strahlensatz
gedruckt am 08. Jul. 2025
In der antiken Geometrie wurde bereits sehr früh ein bemerkenswerter Zusammenhang entdeckt, der als Strahlensatz bezeichnet wird: In einem rechtwinkeligen Dreieck sind die Verhältnisse zweier Seiten zueinander konstant, wenn bei gleichen Winkeln die Seitenlängen variieren.
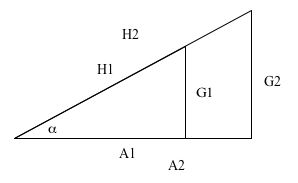
Skizze: Hypothenuse, Gegenkathete, Ankathete bzw. Strahlensatz
Untersucht man diesen Zusammenhang etwas systematischer, so kann man folgende Sachverhalte feststellen und definieren:
- Wird der Winkel Alpha größer (von 0° bis 90°), so wird auch das Verhältnis G:H größer, es erhält Werte von 0 bis 1.
- Wird der Winkel Alpha größer (von 0° bis 90°), so wird das Verhältnis A:H kleiner, es erhält Werte von 1 bis 0.
- Aufgrund des Satzes von Pythagoras gilt: (G:H)2 + (A:H)2 = 1.
- Wird der Winkel Alpha größer (von 0° bis 90°), so wird das Verhältnis von G:A größer, ist allerdings bei 90° nicht mehr definiert (da hier A=0).
Historisch hat sich die Verwendung genau dieser genannten Seitenverhältnisse durchgesetzt. Diese Seitenverhältnisse wurden folgendermaßen benannt: (a steht für Alpha)
G:H heißt Sinus von Alpha: sin(a),
A:H heißt Cosinus von Alpha: cos(a),
G:A heißt Tangens von Alpha: tan(a).
G:A als tan(a) beschreibt übrigens die Steigung einer Geraden.
Begriffe
G ist die Winkel a gegenüberliegende Seite, A die dem Winkel a anliegende Seite. H ist die Hypothenuse, die längste Seite im rechtwinkeligen Dreieck und liegt dem rechten Winkel gegenüber.
Arbeitsanregung
- Skizziere ein paar rechtwinkelige Dreieecke und benenne H, G, A und a. Gib an, welche Seitenverhältnisse Sinus, Cosinus und Tangens beschreiben!
- Zeichne je ein rechtwinkeliges Dreieck mit H=10cm, H=5cm, H=3cm und Winkel a=30°. Berechne jeweils sin(a), cos(a) und tan(a) und beobachte, dass das Seitenverhältnis von der Länge der Hypothenuse abhängen.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 