Die Logarithmusfunktion
gedruckt am 24. Dec. 2025
Wir haben den Logarithmus als Rechenart kennengelernt. Nehmen wir jetzt den Logarithmus zur Basis 10 und berechnen verschiedene Werte wie log1, log2, log3, etc. Ordnen wir jetzt den x-Werten 1, 2, 3 ihre (10er-)Logarithmen (als y-Werte) zu, so erhalten wir die (10er-)Logarithmus-Funktion f(x) = log(x).
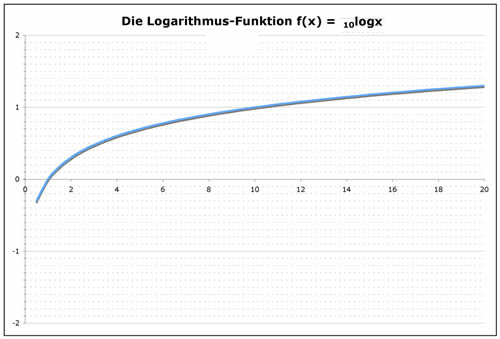
An der grafischen Darstellung kann man recht gut die Zusammenhänge beim Logarithmus sehen: log1=0, log10=1, log100=2 etc.
Arbeitsanregungen
- Zeichne die Logarithmus-Funktion f(x)=ldx (Logarithmus zur Basis 2) und beobachte alle dir ersichtlichen Zusammenänge!
- Für welche x-Werte ist die Logarithmus-Funktion nicht definiert?
- Zeichne die Logarithmus-Funktionen für Basis 3, e und stelle Regeln für den Verlauf dieser Funktionen auf: Welche Funktionen verlaufen flacher, steiler, wovon hängt das ab? Gibt es einen gemeinsamen Punkt für alle diese Logarithmus-Funktionen?
- Vergleiche die Logarithmus-Funktionen mit den Exponentielfunktionen gleicher Basis, finde und formuliere Zusammenhänge!
Hinweis und Anregung für eigene Forschungen
Skaliert man die x-Achse logarithmisch (zur Basis 10), so wird die Logarithmus-Funktion (mit Basis 10) als Gerade dargestellt. Entsprechend verhält es sich mit den Log-Funktionen mit anderer Basis. Das zeigt ganz schön die innere Struktur der Logarithmus-Funktion, in jedem ganzzahligen x-Schritt wiederholen sich die y-Schritte, allerdings entsprechend gestreckt… Untersuche selbst, wie das gemeint ist und beachte den Zusammenhang zur Regel … (Siehe Die Gesetze des Logarithmus)


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 