Exponentiell abnehmende Zufallszahlen
gedruckt am 04. Apr. 2025
Vokabel-Lernprogrammm: exponentiell verteilte Zufallszahlen
Für ein Vokabel-Lernprogramm sollen Vokabeln zufällig zur Überprüfung ausgewählt werden. Jene Vokabeln, die bereits ein- oder mehrmals richtig gewusst wurden, sollen weniger oft abgefragt werden.
Schritte zur Realisierung
Wenn eine Vokabel richtig beantwortet wird, erhält die Vokabel einen Punkt, bei falscher Antwort wird ein Punkt (besser: die Hälfte der Punkte) abgezogen. Der Punktebereich ist nach oben nicht begrenzt. Die Vokabeln werden in Reihenfolge der Punktezahl aufsteigend sortiert.
Der mathematische Hintergrund
Zufallszahlen sind bei Computerprogrammen grundsätzlich gleich verteilt, jede Zufallszahl kommt gleich oft vor, wenn nur oft genug gewürfelt wird. In unserem Fall soll die Häufigkeit der Auswahl in Abhängigkeit von der Punkteanzahl abnehmend exponentiell verlaufen. Maßgeblich für Auswahl einer Vokabel ist Position in der Reihenfolge, Vokabeln mit einer geringeren Punktezahl stehen vorne und werden häufiger ausgewählt, weil kleinere Zufallszahlen häufiger vorkommen.
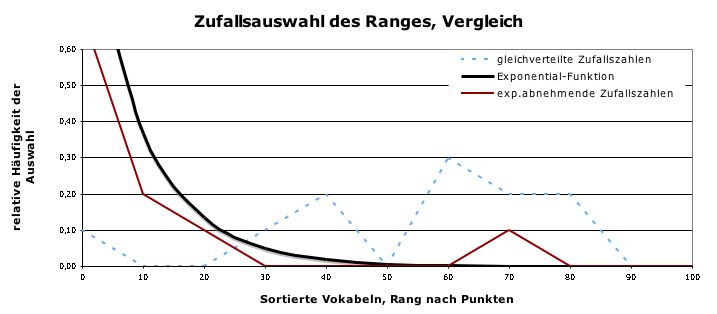
Die Häufigkeiten von 10 Zufallszahlen im Vergleich
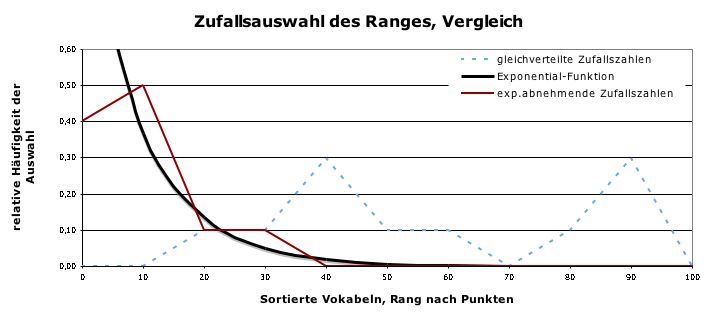
Die Häufigkeiten von 10 Zufallszahlen im Vergleich
Die Skizze zeigt 10 Zufallszahlen, und zwar gleichverteilte Zufallszahlen und exponentiell abnehmende Zufallszahlen, dazu noch die entsprechende Exponentialfunktion.
Die Berechnung der exponentiell abnehmenden Zufallszahlen
Ich habe die Formel für EXCEL realisiert und erkläre sie schrittweise:
=ZUFALLSZAHL() ergibt eine gleichverteilte Zufallszahl zwischen 0 und <1.
=ZUFALLSZAHL()*Anzahl+1 .. Zufallszahl zwischen 1 und Anzahl. Anzahl ist die Anzahl der Vokabeln in der Liste.
Diese Zahl wird logarithmiert:
=LOG(ZUFALLSZAHL()*Anzahl+1) … Zufallszahl zwischen 0 und LOG(Anzahl).
Damit das Intervall dieser logarithmierten Zufallszahl bei Null beginnt, wird im Schritt vorher die Eins addiert. Da die Logarithmen der Zahlen von 1 bis Anzahl unterschiedliche (nach oben hin größere) Abstände haben, kommen die größeren Werte häufiger vor.
Damit das Intervall wieder von 0 bis Anzahl reicht, wird die Zufallszahl mit Anzahl/LOG(Anzahl) multimpliziert, das streckt das Intervall auf 0 bis Anzahl.
=LOG(ZUFALLSZAHL()*Anzahl+1)*Anzahl/LOG(Anzahl)
Da nicht die größeren Werte, sondern die kleineren Werte häufiger ausgewählt werden sollen, subtrahiere ich die erhaltene Zufallszahl von der Anzahl der Vokabeln:
=Anzahl-LOG(ZUFALLSZAHL()*Anzahl+1)*Anzahl/LOG(Anzahl)
Um nur ganzzahlige Werte zu erhalten, wird das Ergebnis gerundet:
=Anzahl-RUNDEN(LOG(ZUFALLSZAHL()*Anzahl+1)*Anzahl/LOG(Anzahl))
Das ist die Formel für exponentiell abnehmende Zufallszahlen, das Ergebnis ist der Rang der gewählten Vokabel.
Weitere Anwendungen für exponentiell abnehmende Zufallszahlen
Dieses Konzept der ungleichmäßigen Zufallsauswahl könnte sich auch (Mathematik-)Lehrer für die Auswahl zu prüfender Schüler/innen zunutze machen, wobei die Schüler/innen nach Leistung aufsteigend (die schlechten sind in der Liste vorne) sortiert werden …
Ein Komponist will ein Zufallsmusikstück schreiben. Er könnte nach dem Motto vorgehen lange Noten kommen seltener vor, kurze Noten häufiger oder kleine Intervallschritte kommen häufiger vor, große Sprünge seltener…
Als Medienkünstler arbeite ich an folgendem Projekt: Eine Videokamera nimmt Passant/innen vor der Kamera in Kurzvideos auf. Diese Clips werden gespeichert und mit Aufnahmen früherer Passant/innen gemischt und projiziert. Dabei sollen neuere Videos öfter zum Mischen ausgewählt werden als bereits länger zurückliegende Clips. Die Clips werden mit Datum und Uhrzeit als Dateinamen automatisch gespeichert und in eine Auswahlliste nach Dateinamen sortiert, exponentiell abnehmende Zufallszahlen wählen die Clips zum Mischen aus und die neueren Clips kommen daher häufiger vor.
Sicherlich gibt es weitere Anwendungsmöglichkeiten.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 