Berechnung der Ableitungsfunktion: Grenzwertrechnung
gedruckt am 04. Apr. 2025
Die Berechnung der Tangentensteigung gelingt mit Hilfe der Grenzwertrechnung. Das Problem ist ja, dass die Tangentensteigungen nicht von vornherein klar sind, sondern sie über die Bestimmung von Sekanten, deren x-Werte beliebig nahe beisammen liegen, näherungsweise bestimmt werden müssen.
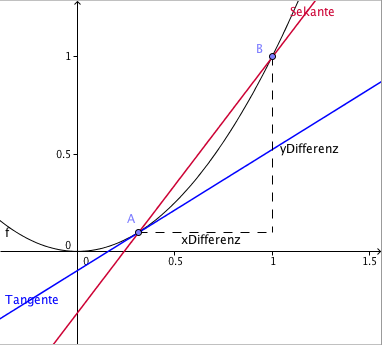
Tangente bzw. Sekante: Je näher der obere Punkt B zum Punkt A auf der quadratischen Funktion geschoben wird, umso kleiner das Steigungsdreieck und umso mehr neigt sich die Sekante zur Tangente.
Schiebt man A einfach auf B, dann sind yDifferenz und xDifferenz der beiden Punkte jeweils Null und die Steigung müßte mit Hilfe der Division 0/0 berechnet werden. Diesem Dilemma entgeht die Mathematik mit der Entwicklung der Grenzwertrechnung.
Um die genaue Tangentensteigung zu berechnen, berechnet man zuerst eine Folge von Näherungen (Sekantensteigungen), wobei darauf geachtet wird, dass das Intervall der x-Werte systematisch verkleinert (etwa halbiert) wird. In diesem Fall kann man beobachten, dass die Folge der Näherungssteigungen ebenfalls einer Systematik unterliegt und einem bestimmten Wert (Grenzwert) zustrebt. Die Grenzwertrechnung stellt dann die entsprechenden Regeln (Limes einer Folge) zur Verfügung.
Didaktische Anmerkung
Ich verzichte am Beginn der Differentialrechnung auf die Grenzwertrechnung, da die geometrische Ableitung von Funktionen evident genug ist und die Grenzwertrechnung vom Thema zu sehr ablenkt. Nach der Analyse von Funktionen (Funktionsdiskussion) und Anwendungen (Kostentheorie, Taylor-Näherungsfunktionen) kann ich noch gut zur Grenzwertrechnung zurückkommen.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 